Appendix A — Formulae
A.1 Rules of Cosine and Sine
\[ c^2 = a^2 + b^2 - 2ab\cos \gamma \] \[ \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} \]
A.2 Linear Motion
\[ \vec{v} = \vec{u} + \vec{a}t \]
\[ \vec{s} = \frac{\vec{u}+\vec{v}}{2}t \]
\[ \vec{s} = \vec{u}t + \frac{1}{2}\vec{a}t^2 \]
\[ \vec{v}^2 = \vec{u}^2 + 2\vec{a} \cdot \vec{s} \]
where:
- \(\vec{u}\): Initial velocity
- \(\vec{v}\): Final velocity
- \(\vec{s}\): Displacement
- \(\vec{a}\): Acceleration
- \(t\): Time
A.3 Angular Motion
\[ \omega_2 = \omega_1 \mp \alpha t \]
\[ \theta = \frac{\omega_1+\omega_2}{2}t \]
\[ \theta = \omega_1 t \mp \frac{1}{2}\alpha t^2 \]
\[ \omega_2^2 = \omega_1^2 \mp 2\alpha \theta \]
where:
\(\omega_1\): Initial angular velocity (rad/s)
\(\omega_2\): Final angular velocity (rad/s)
\(\theta\) Angular displacement (rad)
\(\alpha\): Angular acceleration (rad/s2)
\(t\): Time (s)
A.4 Relation Between Linear and Angular Motion
The relationship between linear and angular motion is described by the following equations:
\(s = r \theta\) (linear displacement \(s\) and angular displacement \(\theta\)).
\(v = r \omega\) (linear velocity \(v\) and angular velocity \(\omega\)),
\(a = r \alpha\) (linear acceleration \(a\) and angular acceleration \(\alpha\)).
A.5 Centre of Gravity
\[ \bar{x} = \frac{ \sum Moments\ of\ Weights}{\sum Weights} \qquad \bar{y} = \frac{ \sum Moments\ of\ Weights}{\sum Weights} \]
A.6 Centroid
\[ \bar{x} = \frac{ \sum {\bar{x}_i}\ A_i}{\sum A_i} \qquad \bar{y} = \frac{ \sum {\bar{y}_i}\ A_i}{\sum A_i} \]
A.7 Parallel Axis Theorem
To find the moment of inertia about an axis parallel to the centroidal axis:
\[ I = I_c + A d^2 \]
A.8 Radius of Gyration
\[ k = \sqrt{\frac{I}{A}} \quad \text{(for area)} \quad \text{or} \quad k = \sqrt{\frac{I}{m}} \quad \text{(for mass)}, \]
where:
\(I\): Moment of inertia about the axis
\(A\): Area of the cross-section (for area calculations)
\(m\): Mass of the body (for mass calculations)
A.8.1 Rectangle (about its centroidal axis)
Dimensions: ( b ) (breadth), ( h ) (height)
Radius of gyration about the centroidal x-axis: \[ k_x = \sqrt{\frac{I_x}{A}} = \sqrt{\frac{\frac{1}{12} b h^3}{b h}} = \frac{h}{\sqrt{12}} \]
A.8.2 Circle (about its centroidal axis)
Radius: ( r )
Radius of gyration: \[ k = \sqrt{\frac{I}{A}} = \sqrt{\frac{\frac{\pi r^4}{4}}{\pi r^2}} = \frac{r}{\sqrt{2}} \]
A.9 Beam Calculations
| Sum of Horizontal Forces | Sum of Vertical Force | Sum of Moments |
|---|---|---|
| \(\sum F_x = 0\) | \(\sum F_y = 0\) | \(\sum M = 0\) |
| Load Type | Shear Diagram Shape | Moment Diagram Shape |
|---|---|---|
| Point Load | Rectangular (constant) | Triangular |
| Uniformly Distributed Load (UDL) | Triangular | Parabolas (second degree) |
A.10 Dynamics
A.10.1 Linear momentum
\[ Linear\ momentum = m \vec{v} \]
Where:
Linear momentum is in kg·m/s.
\(m\) is the mass of the object in kilograms.
\(\vec{v}\) is the velocity of the object in meters per second.
A.10.2 Angular momentum
\[ \text{Angular momentum} = I \omega \]
Where:
- \(I\) is the moment of inertia in \(m^4\).
- \(\omega\) is the angular velocity in \(rad/s\).
A.10.3 Moment of inertia
\[ I = m k^2 \]
Where:
- \(I\) is the moment of inertia in \(m^4\).
- \(m\) is the mass in \(kg\).
- \(k\) is the radius of gyration in \(m\).
A.10.4 Turning moment
\[ \tau = I \alpha \]
Where:
- \(\tau\) is the torque in \(Nm\).
- \(I\) is the moment of inertia in \(m^4\).
- \(\alpha\): Angular acceleration in \(rad/s^2\).
A.10.5 Power by Torque
\[ P = \tau \cdot \omega \]
Where:
\(P\) is the power in watts (W),
\(\tau\) is the torque in newton-meters (Nm), and
\(\omega\) is the angular velocity in radians per second (rad/s).
A.10.6 Kinetic Energy of Rotation
\[ \text{Rotational K.E.} = \frac{1}{2} I \omega^2 \] Where:
\(I\) is the moment of inertia in \(m^4\).
\(\omega\) is the angular velocity in radians per second (rad/s).
A.11 Stress and Strain
A.11.1 Stress
\[ \sigma = \frac{F}{A} \]
\[ \tau = \frac{F}{A} \]
Where:
\(\sigma\) is the stress (Pa),
\(\tau\) is the shearing stress (Pa),
\(F\) is the shearing force (N),
\(A\) is the cross-sectional area (m\(^2\)).
A.11.2 Strain
\[ \varepsilon = \frac{\Delta L}{L_0} \]
Where:
\(\varepsilon\) is the strain (unitless),
\(\Delta L\) is the change in length,
\(L_0\) is the original length.
A.11.3 Hooke’s Law
\[ E = \frac{\sigma}{\varepsilon} \]
Where:
- \(\sigma\) is the stress (Pa).
- \(\varepsilon\) is the strain (unitless).
- E: Young’s modulus (Pa), a material property (modulus of elasticity).
A.11.4 Factor of Safety (FOS)
\[ \text{FOS} = \frac{\text{Breaking Stress}}{\text{Working Stress}} \]
A.12 Hydrodynamics
A.12.1 Volume Flow
\[ \dot{v} = A \cdot C \]
Where:
\(\dot{v}\): Volume flow rate, \(\mathrm{m^3/s}\)
\(A\): Cross-sectional area of the flow, \(\mathrm{m^2}\)
\(C\): Mean (average) velocity of the fluid, \(\mathrm{m/s}\)
A.12.2 Mass Flow
\[ \dot{m} = \rho \cdot \dot v \]
Where:
\(\dot{m}\): mass flow rate, \(\mathrm{kg/s}\)
\(\rho\): density, \(\mathrm{kg/m^3}\)
\(\dot{v}\): volume flow, \(\mathrm{m^3/s}\)
A.12.3 Specific Weight
\[ \gamma = g \cdot \rho \]
Where:
\(\gamma\): specific weight, \(\mathrm{N/m^3}\)
\(g\): gravitational acceleration, \(\mathrm{m/s^2}\)
\(\rho\): density, \(\mathrm{kg/m^3}\)
A.12.4 Continuity Equation
\[ A_1 \cdot C_1= A_2 \cdot C_2 \]
A.12.5 Energy Equation
\[ Z_1+\frac{C_1^2}{2g}+\frac{P_1}{g\rho_1}=Z_2+\frac{C_2^2}{2g}+\frac{P_2}{g\rho_2} \]
\[ Z_1+\frac{C_1^2}{2g}+\frac{P_1}{\gamma_1}=Z_2+\frac{C_2^2}{2g}+\frac{P_2}{\gamma_2} \]
Each term has units of m, therefore:
Potential energy \(Z\) is known as the elevation head.
Kinetic energy \(\frac{c^2}{2g}\) is known as the velocity head.
Pressure energy \(\frac{P}{\gamma}\) is known as the pressure head.
\[ Total\ Head= Elevation\ Head + Velocity\ Head + Pressure\ Head \]
A.12.6 Bernoulli’s Equation
\[ P_1 + \frac{1}{2} \rho C_1^2 + \rho g h_1 = P_2 + \frac{1}{2} \rho C_2^2 + \rho g h_2 \]
Where:
\(P_1\) and \(P_2\) are the pressures at points 1 and 2, respectively.
\(\rho\) is the density of the fluid.
\(C_1\) and \(C_2\) are the velocities of the fluid at points 1 and 2, respectively.
\(g\) is the acceleration due to gravity.
\(h_1\) and \(h_2\) are the heights of the fluid at points 1 and 2, respectively.
| Shape | Area | \(\bar{x}\) | \(\bar{y}\) |
|---|---|---|---|
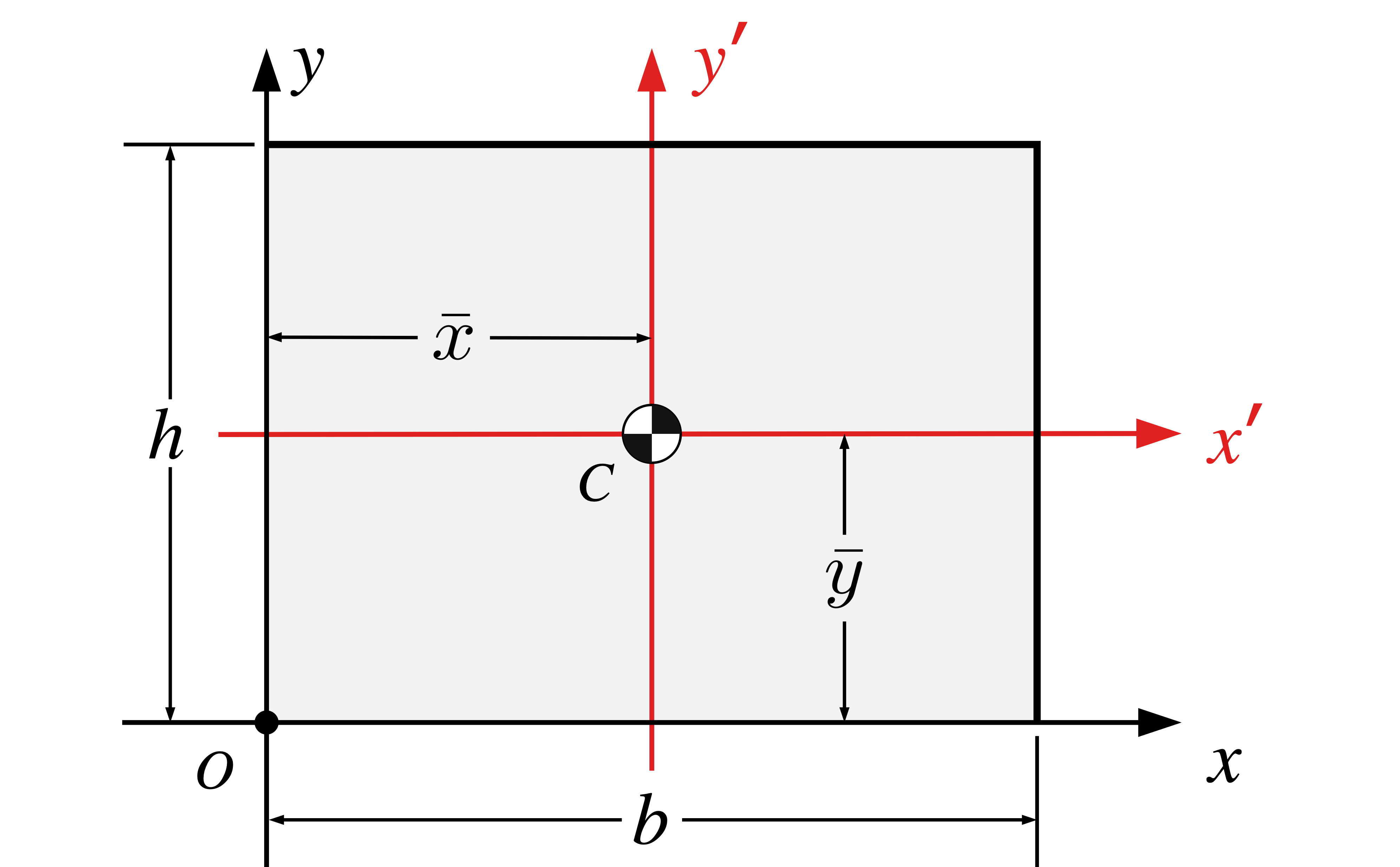 |
\(A = b h\) | \(b/2\) | \(h/2\) |
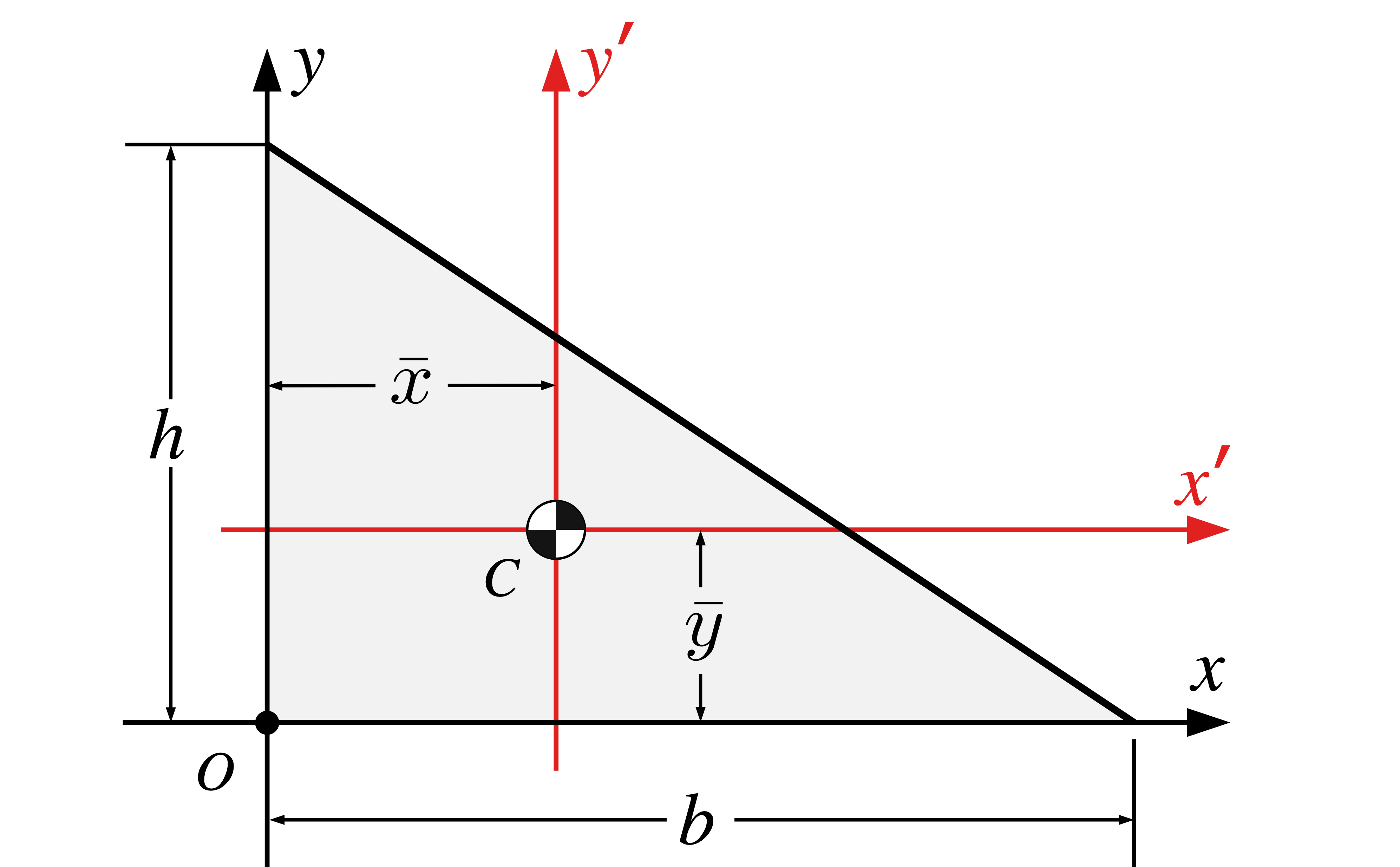 |
\(\dfrac{bh}{2}\) | \(b/3\) | \(h/3\) |
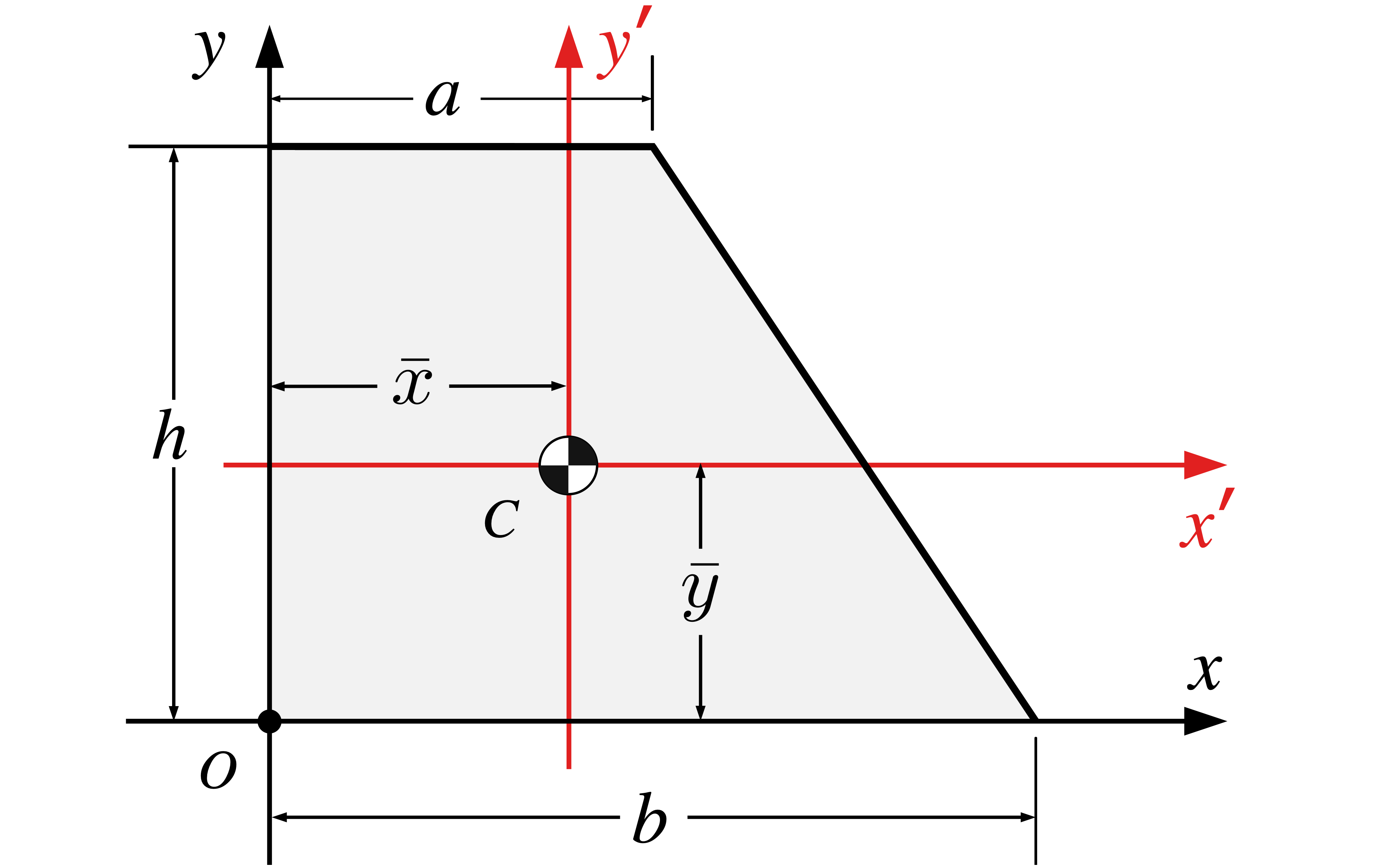 |
\(\dfrac{(a+b) h}{2}\) | \(\dfrac{a^2 +ab + b^2}{3 (a+b)}\) | \(\dfrac{h(2a+b)}{3(a+b)}\) |
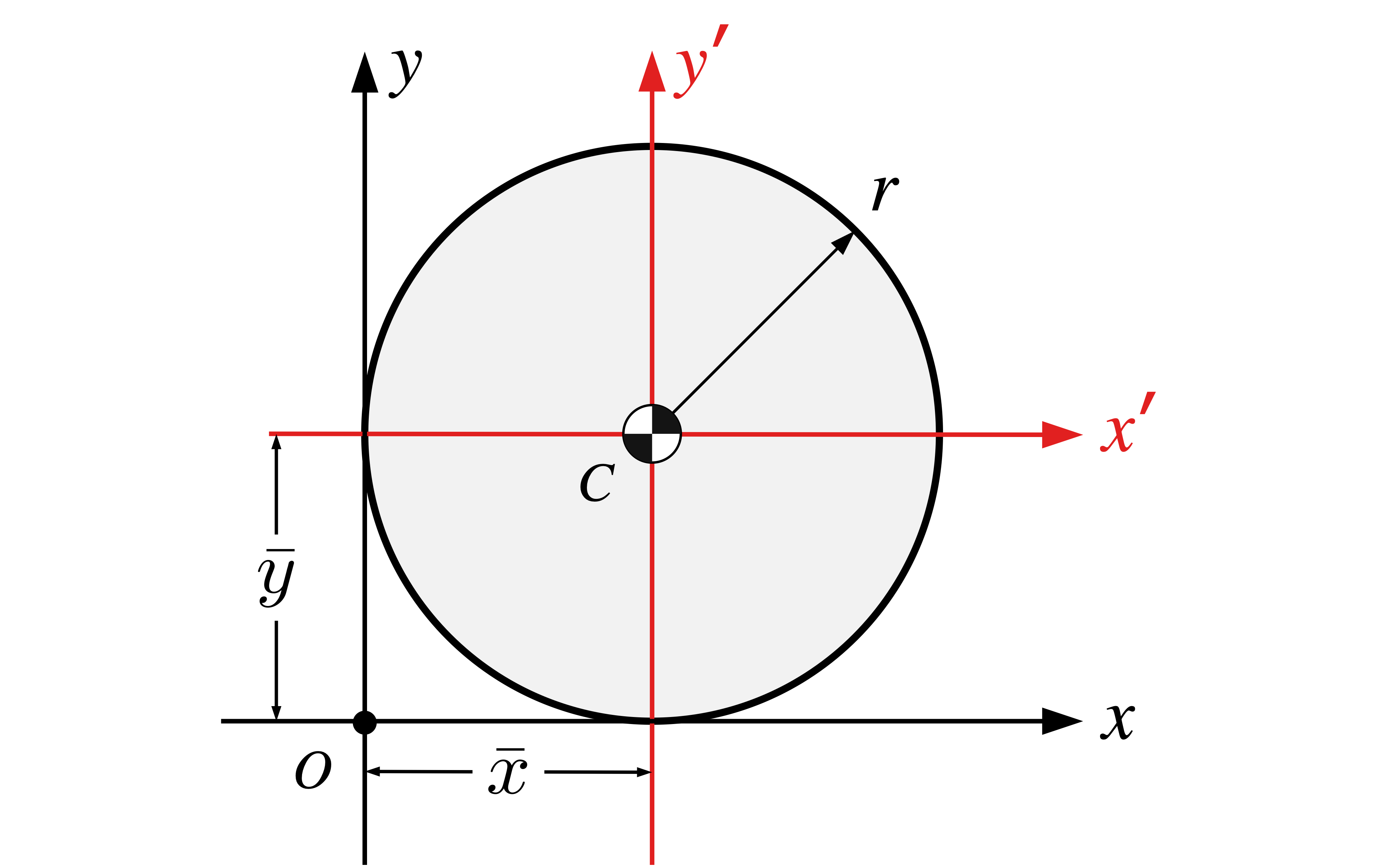 |
\(\pi r^2\) | \(r\) | \(r\) |
 |
\(\dfrac{\pi r^2}{2}\) | \(r\) | \(\dfrac{4 r}{3 \pi}\) |
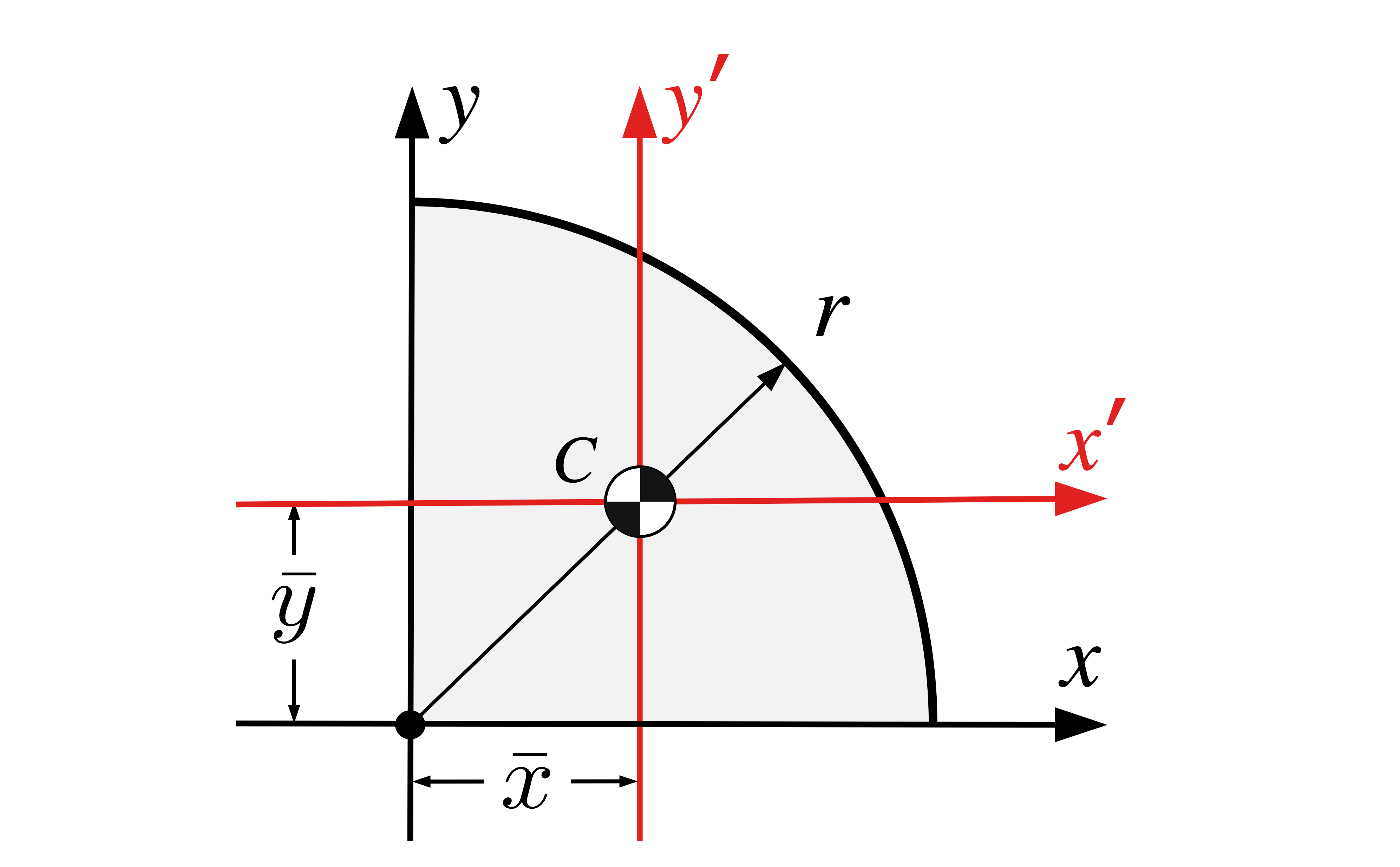 |
\(\dfrac{\pi r^2}{4}\) | \(\dfrac{4 r}{3 \pi}\) | \(\dfrac{4 r}{3 \pi}\) |
A.13 Second Moments of Common Shapes
| Shape | Second moment (\(I_x\)) | Second moment (\(I_y\)) |
|---|---|---|
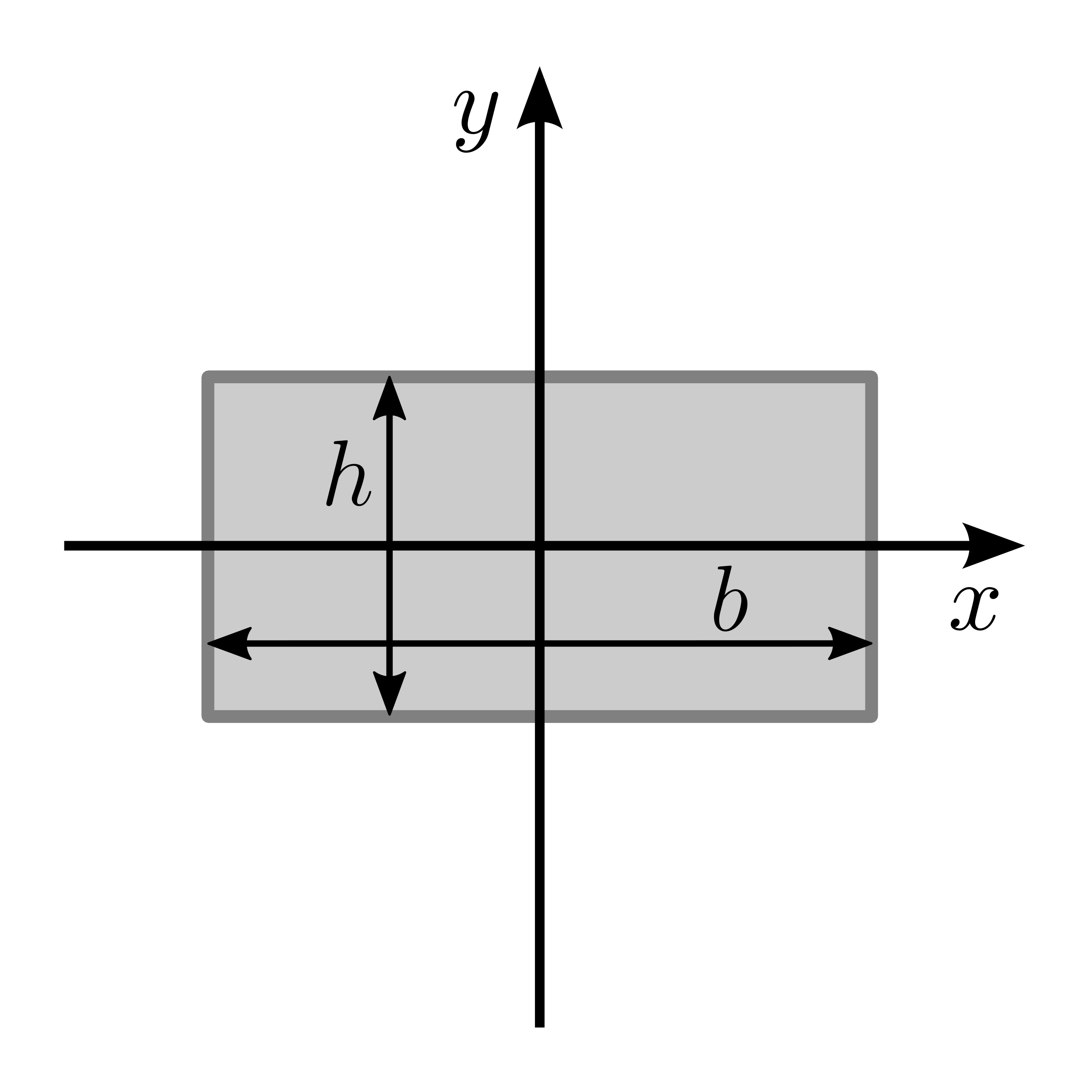 |
\(I_x = \frac{1}{12} b h^3\) | \(I_y = \frac{1}{12} b^3 h\) |
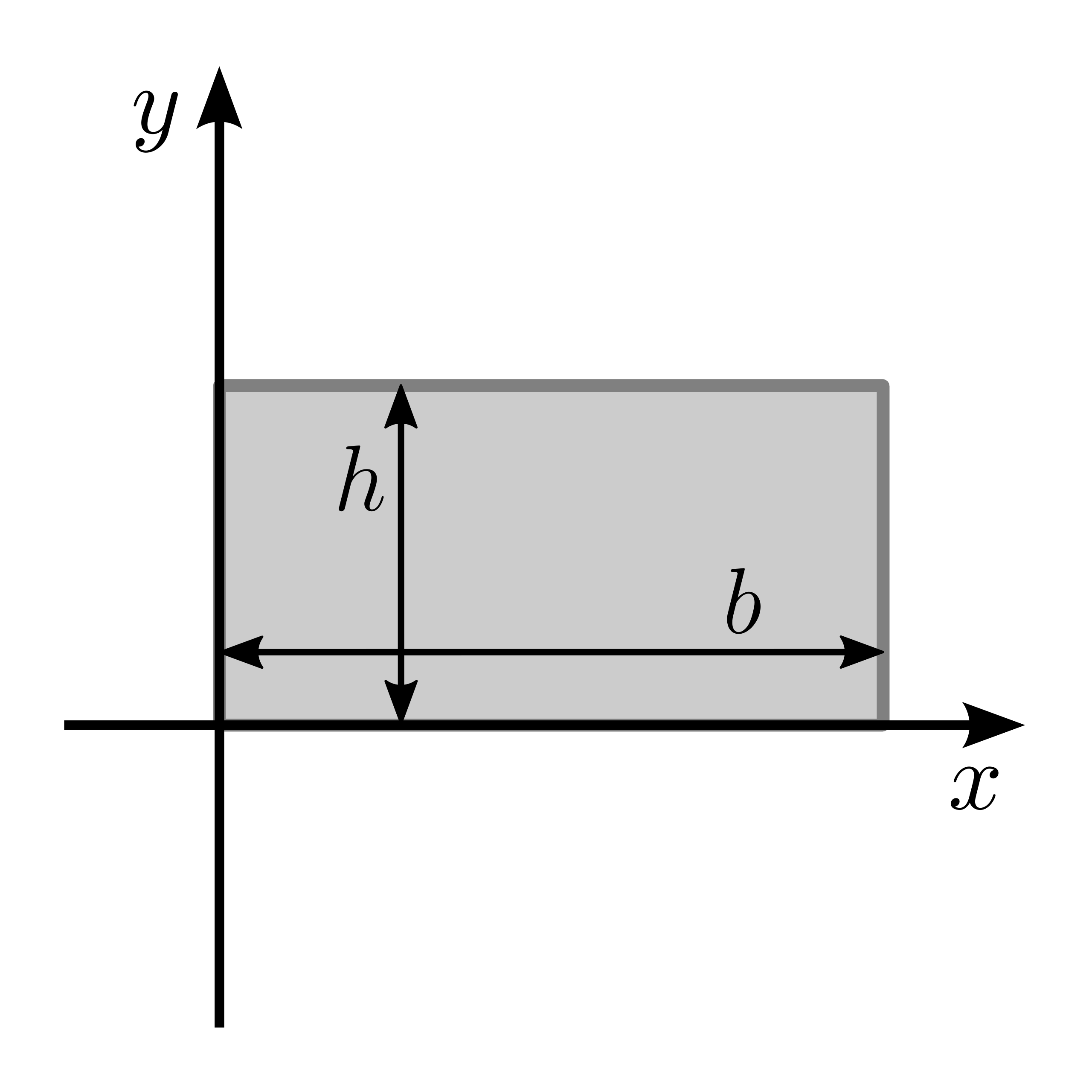 |
\(I_x = \frac{1}{3} b h^3\) | \(I_y = \frac{1}{3} b^3 h\) |
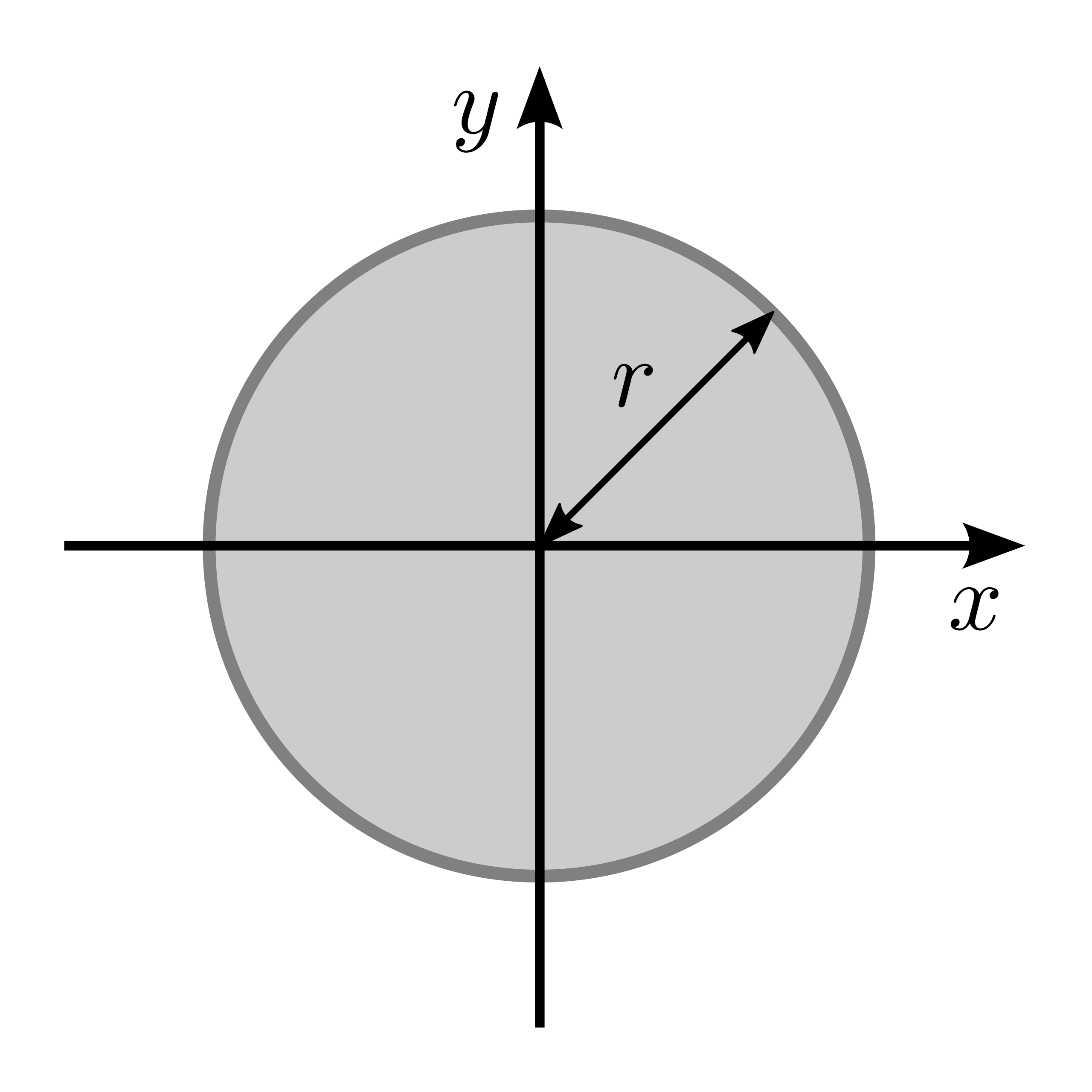 |
\(I_x = \frac{\pi}{4} r^4\) | \(I_y = \frac{\pi}{4} r^4\) |
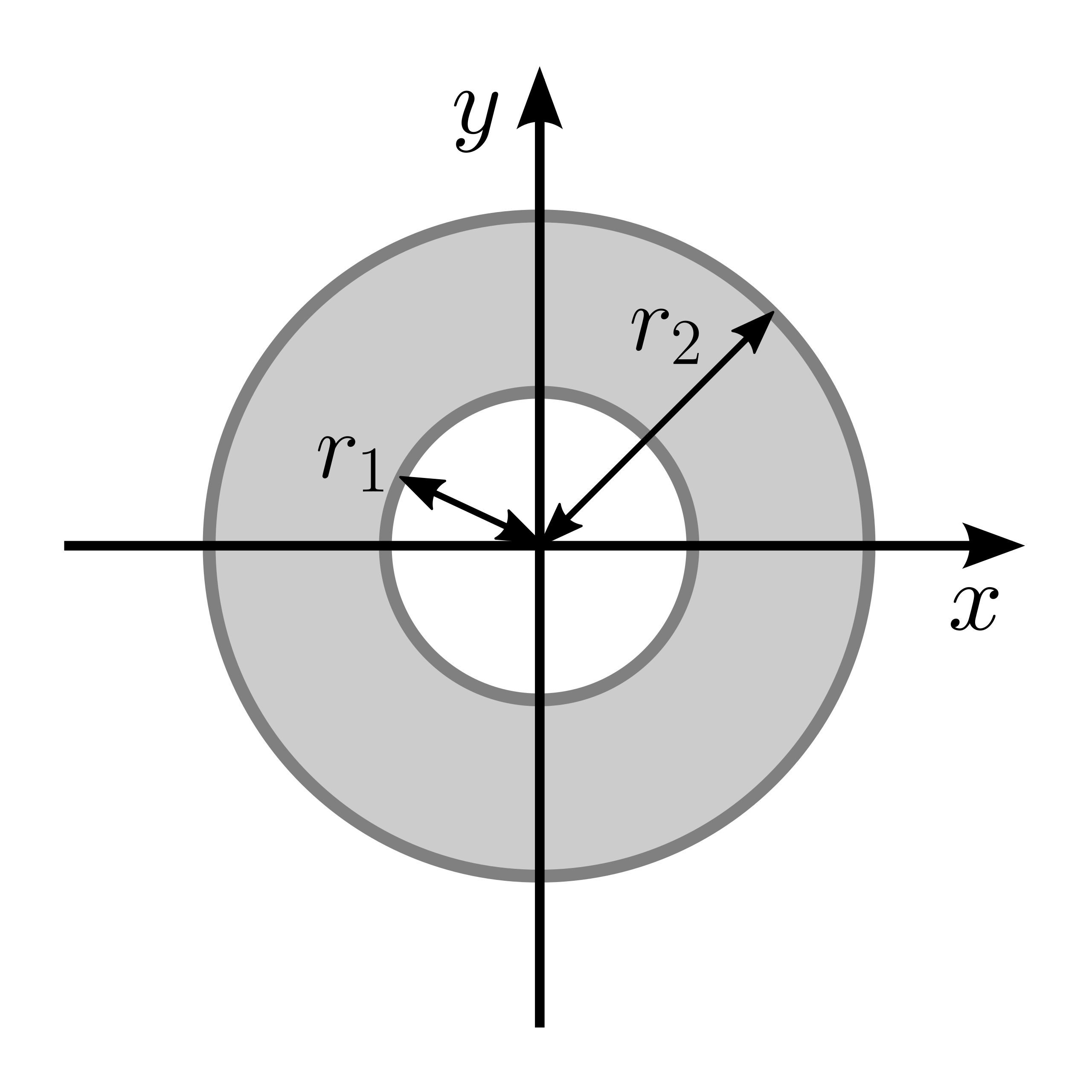 |
\(I_x = \frac{\pi}{4} (r_2^4-r_1^4)\) | \(I_y = \frac{\pi}{4} (r_2^4-r_1^4)\) |
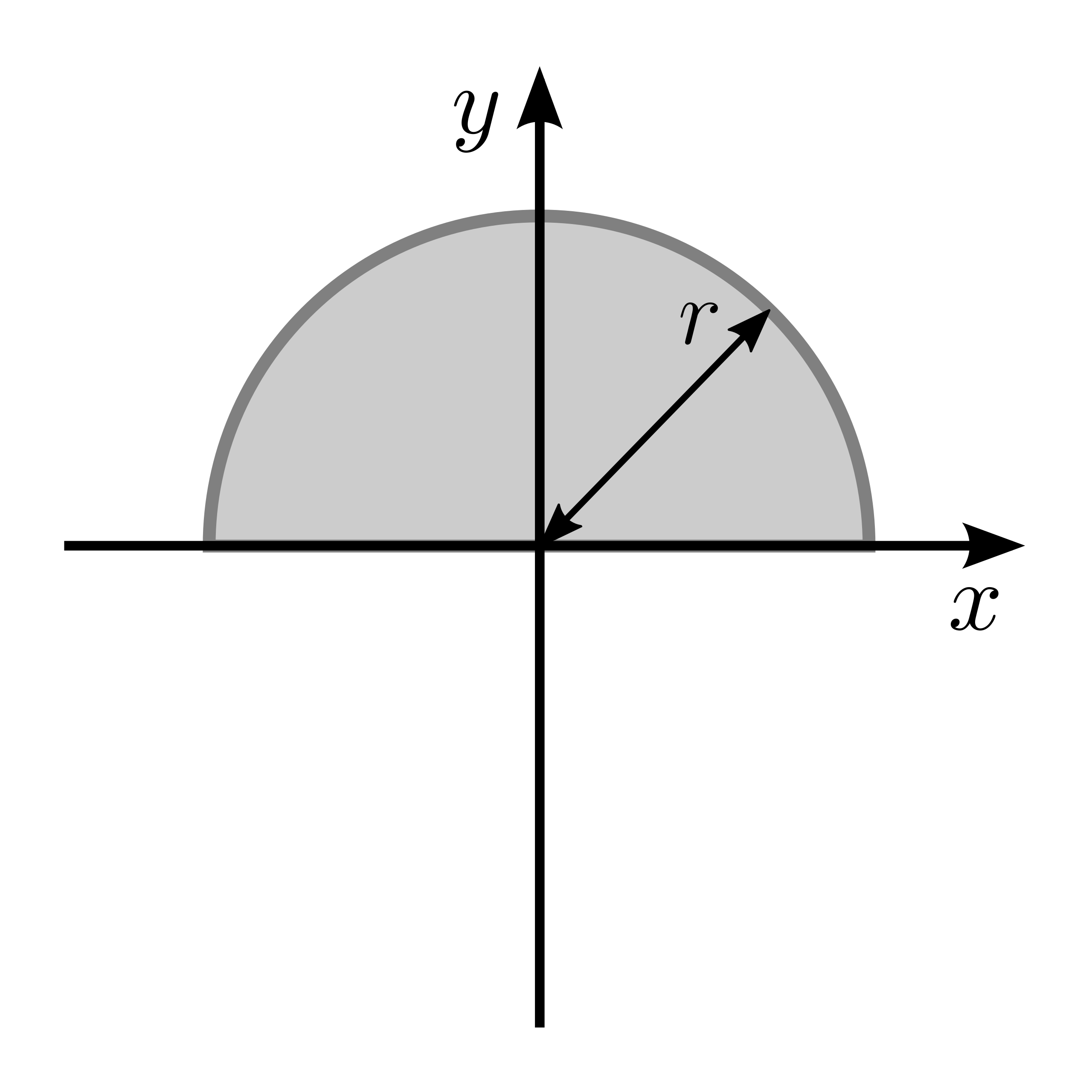 |
\(I_x = \frac{\pi}{8} r^4\) | \(I_y = \frac{\pi}{8} r^4\) |
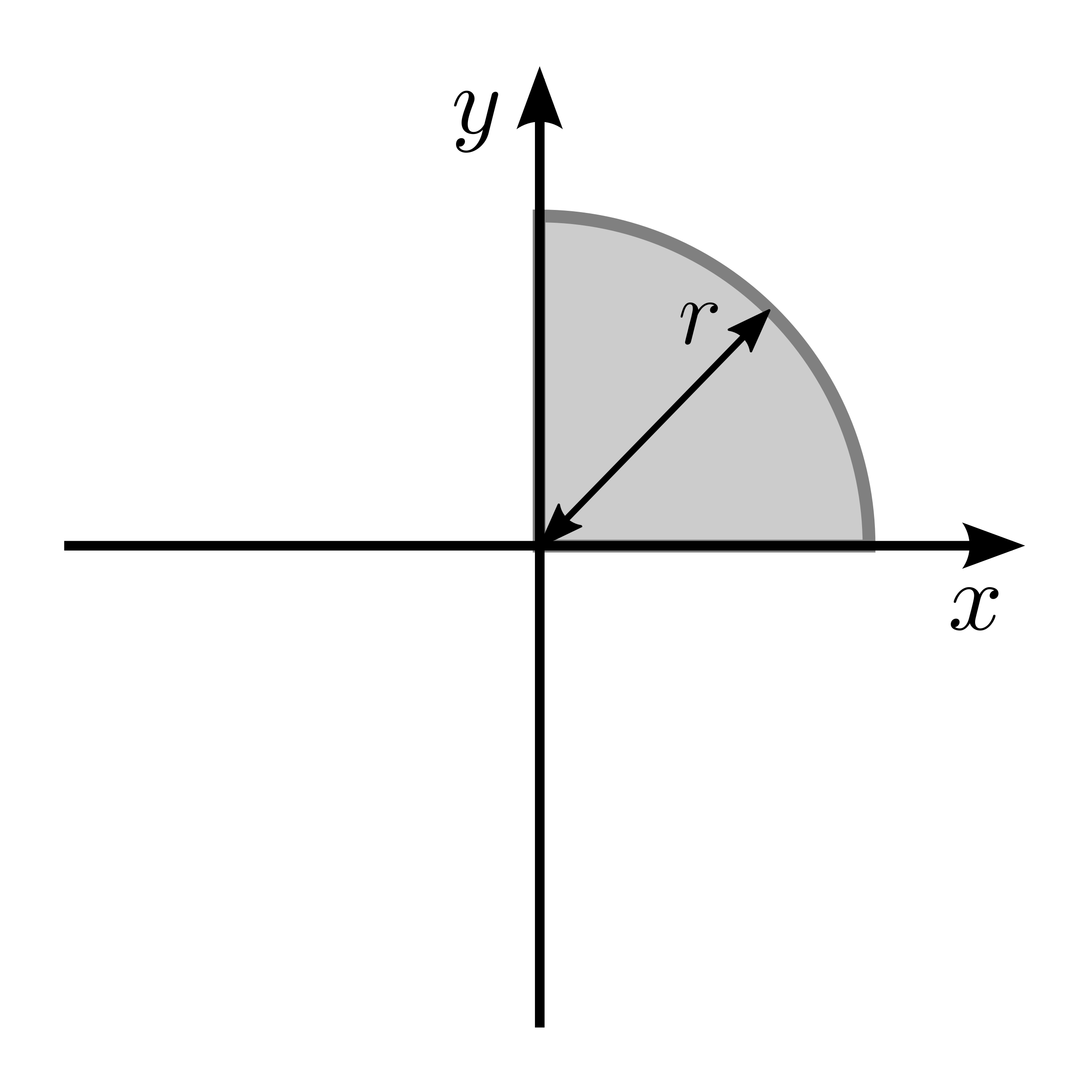 |
\(I_x = \frac{\pi}{16} r^4\) | \(I_y = \frac{\pi}{16} r^4\) |
 |
\(I_x = \frac{1}{12} b h^3\) | |
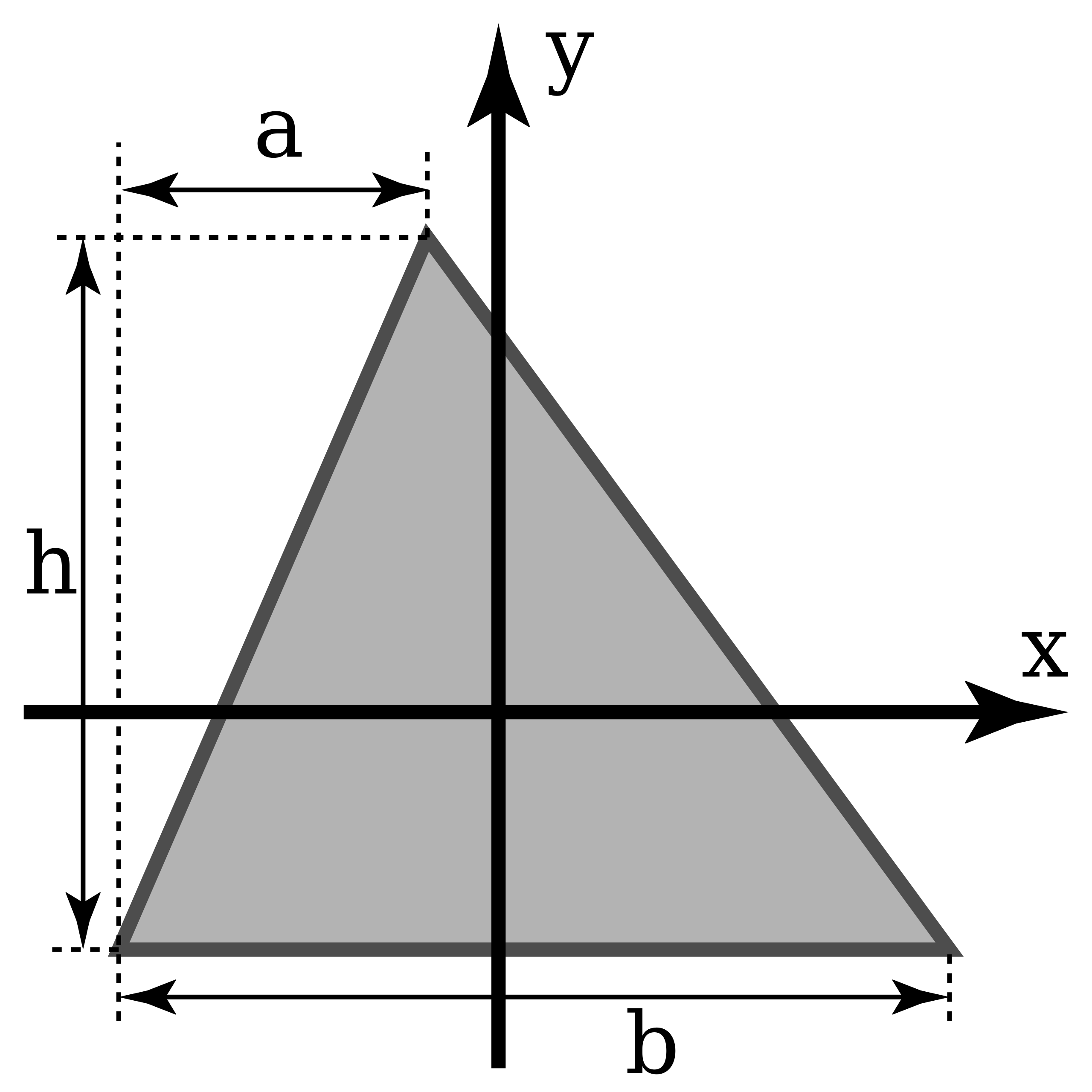 |
\(I_x = \frac{1}{36} b h^3\) |